I'm happy to announce that my software rasterizer side project has been picked up by a major commercial VR product a while ago. While I can't go into too much detail, adding in the rasterizer gave an average frame time saving of 1ms on the CPU and GPU each, which was critical to shipping the product on the targetted min spec configuration. There's some unique challenges in using this in practice which I'm going to address as part of this post, as well as going into some details regarding the next release of the rasterizer which brings a ~1.5x speedup compared to the initial release. Because real life has forced me to delay this post a bit, it covers both commits https://github.com/rawrunprotected/rasterizer/commit/d2fa65fd6b5df8b94d8d4b02914354c9aca2d46d and https://github.com/rawrunprotected/rasterizer/commit/ca469a402a65341a37c692ed06b4d355fe6d5494, even those are almost a year apart.

Over-occlusion in VR

Using software occlusion culling in 3D graphics typically involves some amount of false negatives; i.e. queries returning that an object is occluded even though it should be visible on screen. The reason for that is that software rasterization is generally performed on a lower resolution than the target render resolution. Unless the rasterizer is written "to spec" and matches the behavior of the hardware graphics API exactly, it may also introduce additional error through differences in vertex quantization or edge test precision.

This isn't much of a problem in practice for flat-screen applications as long as the incorrect over-occlusion can be kept below some threshold, say 5 pixels, which is barely noticeable to the user. In VR however, lens distortion implies that angular resolution is much lower, particularly in the center of the screen. This makes even small over-occlusion artifacts very noticable. Another problem is that it's not practical to perform occlusion for both eyes each frame, and it is easy to construct cases where culling only for one eye or a synthetic camera position centered between the eyes fails completely. Applying occlusion culling naively led to some user complaints in the initial beta release of the product as there were some geometric constellations which would result in noticable artifacts.

A simple approach to both of these issues is to apply a simple form of temporal filtering. For monoscopic rendering, applying a small amount of sub-pixel camera jitter helps break quantization errors. The jitter pattern repeats over a small period N (e.g. 4 frames), and an object is only considered culled when occlusion queries fail for all N of these frames. The standard MSAA sample distributions work well in practice as jitter patterns. This is fairly cheap to implement by means of a simple counter per object. While it has the disadvantage of introducing a small delay before objects can be culled, it solves the false negative problem for all practical purposes even when downscaling the target resolution by a factor of 5 in both X and Y.

The same can then be extended to stereoscopic rendering, by culling against left and right eye in alternating frames; doubling the effective length of the jitter period. As this is effectively fully external to the usage of the rasterizer and I'm not at liberty to publish the code anyway, I won't include the temporal filtering approach in the public release.

Another source of errors occurs when the camera moves close enough to near-clip the geometry. While this should ideally be prevented on a higher level as in can result in comfort issues in VR, it produces artifacts as the rasterizer does not perform near-clipping, which allows the user to peek through geometry and see objects flickering in and out of existence. As full emulation of near-clipping is infeasible for performance reasons, a simple hack solves this problems: Pixels which are in front of the near plane are clamped to depth values of 0xFFFF by the rasterizer, so simply adding 1 to each value forces these pixels to wrap around to the far plane, effectively discarding them. The near resulting clipping edge doesn't fully match the GPU result, but is good enough to avoid major discrepancies.

Now for the optimizations in the latest version:

Triangle setup optimizations

The first version of the rasterizer required AVX2, but performed vertex transform and triangle setup only at SSE widths (i.e. 4 in parallel). This has been extended to the full AVX vector width so that 8 triangles are set up in parallel, and the vertex packing format has been adapted accordingly. This results in a rather modest performance increase as it reduces the average utilization per vector, since it's much less likely to discard an entire batch of triangles via back face culling, but it's a net win overall.

An interesting trick was to remove most of the masking on decoding vertices from the packed 11/11/10 vertex format which shaves of a few instructions in the vertex transform portion. For transforming the X component, rather than right-shifting to remove the Y and Z component, I'm now applying the equivalent scale of 1.0f / (1u << 21) as part of the projection matrix. This result in some bleedover of the Y and Z components that were previously masked out, into the X component, so the meshes end up slightly skewed. This effect however can be cancelled by applying the inverse skew to the projection matrix. Making use of the _mm256_broadcast_ss allows keeping most of the projection matrix in memory, which reduces register pressure during the vertex transformation. The rest of the triangle setup code has received a bit of cycle shaving by moving around constant factors, so that the entire portion that translates the edge equations into block space is now removed.

Advanced transposition

A side effect of the wider triangle setup is that transposing the data from triangle-parallel to pixel-parallel layout becomes much harder, as AVX shuffle operations typically operate on each sub-lane of 4 elements separately. This implies having to extract and store each lane to memory separately. However, we can also restrict the shuffle operations to be incomplete, and store data to memory without the full sequence of operations, which effectively changes the order of triangles within each batch. Modifying the primitive index lets us iterate over the triangles in each batch in a changed order, but saving quite a few instructions for transposition.

Fully unrolled coverage mask generation

Similar to the triangle setup, the critical inner loop code was restricted to 4-wide SSE. The main obstacle to widening this was the fact that the _mm256_packus_epi32 operation did not operate on 8 lanes in parallel, resulting in some unintentional interleaving. This was fixed by pre-applying a permutation to each rasterization table entry, allowing the transfer from a single 64bit mask to 4 16x16bit depth masks in a few instructions.

 

Fast clears

This is a simple optimization employed by virtually every hardware rasterizer. Rather than resetting the full-resolution depth buffer to the far plane, we only mark blocks as cleared, which saves significant amounts of bandwidth. Before the previously mentioned unrolled coverage mask generation, this didn't yield much benefit, but now allows squeezing out a few extra percentage points. Since we can't afford an extra buffer to store tile metadata, fast cleared blocks are marked in the HiZ buffer with the value 1. This value is extraordinarily unlikely to be generated during normal operation (compared to using HiZ == 0 which happens all the time), and close enough to 0 so we can ignore falsely culled blocks.

Effectively this change allows us to skip the prior depth load for a large proportion of blocks at the cost of an additional branch for an overall net win. It requires some extra complexity for reading back full depth, but since that is intended for debug visualization only, we can ignore this impact.

 

Complete classification of rasterized quadrilaterals

Now for the meat of the actual original research work. As you may be aware, my rasterizer works with quads rather than triangles (which gives a net benefit as most meshes are authored as quads, which is trivial to recover from a trangle representation).

While convex quadrilaterals are mostly trivial to handle by simply adding a 4th edge equation, this is not the case as soon as non-convex or non-simple vertex quadrilaterals turn up. Until now, the rasterizer handled this with a 5th edge, which splits non-convex quads into two triangles, which are then composed separately. This occurs quite frequently in practice, even if the source data is fully comprised of convex quads, as vertex quantization and rounding errors during perspective projection can easily make any geometry a mess of concave or self-overlapping quads.

Unfortunately, this adds significant overhead for the 5th edge, as well has handling some cases incorrectly. To rectify this, I set out to systematically investigate the properties of possible quads. By exhaustively searching over all possible configurations, I found a total of 25 distinct vertex configurations (rather than the over-simplified 2 cases I handled before). The program I wrote for this breaks my personal complexity record - it is 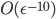in a search error of 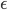, with a total nesting depth of 14 loops.

Describing the complete classification is out of scope for this post, but the important classes are the following ones:

• Culled - occurs for example if both triangles of the quad are backfacing, or in front of the W plane, or a mix of these.
• Convex - the obvious simple case.
• Triangle 0 or triangle 1 culled - the quad is "folded over" so that a single sub triangle is backface culled.
• Concave left or concave right - both sub triangles are forward facing, but with an angle > 180 degrees at either connecting vertex.
• Concave center - some vertices are in front of the camera plane so that the remaining edges form a sort of inifinite W shape, which is extremely rare (< 1 in 1e8 triangles).

All other classes are specialization but can be represented as subsets of these 7. Notably, each of these cases requires only 3 or 4 edge equations to evaluate the covered area, rather than the 5 previously used.

As each configuration can be described only by the signs of the areas of each sub triangle (4 bits including complementary areas) as well as the signs of the W component of each vertex (another 4 bits), a simple lookup table with 16 resp. 256 entries (if any W < 0) allows correctly categorizing each primitive. This lookup is expensive due to the high latency of the gather operation, but allows handling the backface culling and near plane culling tests at the same time, both of which are simply represented by specific entries in the LUT.

Inside the inner-most loop we need to switch over the primitive configuration to determine how to combine the bit masks for individual edge equations. Luckily, the distribution is heavily skewed, with convex primitives being much more likely than the single triangles, which in turn are an order of magnitude more likely to occur than the concave cases. Specializing heavily for the convex case wasn't possible before due to the incorrect handling of some cases, but now yields a significant performance gains. For example, we can now skip evaluation of the edge equations for the rest of a scan line once we enter and leave the covered primitive area.