...sort of.

The core of computing 2D coordinates from a Hilbert index in logarithmic time is a XOR prefix sum. As it so happens, the upper bits of carry-less multiplication with -1 are equivalent to a XOR prefix sum. On an x86 machine with CLMUL and PEXT support, this yields the following "constant time" algorithm for mapping a 32bit Hilbert index to 16bit X and Y:

void hilbertIndexToXY_constantTime(uint32_t i, uint32_t& x, uint32_t& y)
{
	uint32_t i0 = _pext_u32(i, 0x55555555);
	uint32_t i1 = _pext_u32(i, 0xAAAAAAAA);

	uint32_t A = i0 & i1;
	uint32_t B = i0 ^ i1 ^ 0xFFFF;

	uint32_t C = uint32_t(_mm_extract_epi16(_mm_clmulepi64_si128(_mm_set_epi64x(0, 0xFFFF), _mm_cvtsi32_si128(A), 0b00), 1));
	uint32_t D = uint32_t(_mm_extract_epi16(_mm_clmulepi64_si128(_mm_set_epi64x(0, 0xFFFF), _mm_cvtsi32_si128(B), 0b00), 1));

	uint32_t a = C ^ (i0 & D);

	x = (a ^ i1);
	y = (a ^ i0 ^ i1);
}

Of course this isn't really a constant time solution since the CLMUL intrinsic is limited to 64bit operands, and can't be extended to operate on bits in 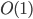time in any reasonable machine model. In practice, this solution also tends to be a hair slower than the logarithmic time solution since both transferring data into/out of SSE registers and the CLMUL intrinsic itself are rather high latency operations.