As referenced in my earlier post about Hilbert curves, it's possible to map between 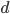-dimensional Euclidean coordinates and the offset along the Hilbert curve in 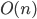time by direct application of the transformation group at each recursion level of the curve. The following applies this to the 3D case:

static const uint8_t mortonToHilbertTable[] = {
	48, 33, 27, 34, 47, 78, 28, 77,
	66, 29, 51, 52, 65, 30, 72, 63,
	76, 95, 75, 24, 53, 54, 82, 81,
	18,  3, 17, 80, 61,  4, 62, 15,
	 0, 59, 71, 60, 49, 50, 86, 85,
	84, 83,  5, 90, 79, 56,  6, 89,
	32, 23,  1, 94, 11, 12,  2, 93,
	42, 41, 13, 14, 35, 88, 36, 31,
	92, 37, 87, 38, 91, 74,  8, 73,
	46, 45,  9, 10,  7, 20, 64, 19,
	70, 25, 39, 16, 69, 26, 44, 43,
	22, 55, 21, 68, 57, 40, 58, 67,
};

static const uint8_t hilbertToMortonTable[] = {
	48, 33, 35, 26, 30, 79, 77, 44,
	78, 68, 64, 50, 51, 25, 29, 63,
	27, 87, 86, 74, 72, 52, 53, 89,
	83, 18, 16,  1,  5, 60, 62, 15,
	 0, 52, 53, 57, 59, 87, 86, 66,
	61, 95, 91, 81, 80,  2,  6, 76,
	32,  2,  6, 12, 13, 95, 91, 17,
	93, 41, 40, 36, 38, 10, 11, 31,
	14, 79, 77, 92, 88, 33, 35, 82,
	70, 10, 11, 23, 21, 41, 40,  4,
	19, 25, 29, 47, 46, 68, 64, 34,
	45, 60, 62, 71, 67, 18, 16, 49,
};

uint32_t transformCurve(uint32_t in, uint32_t bits, const uint8_t* lookupTable)
{
	uint32_t transform = 0;
	uint32_t out = 0;

	for (int32_t i = 3 * (bits - 1); i >= 0; i -= 3) {
		transform = lookupTable[transform | ((in >> i) & 7)];
		out = (out << 3) | (transform & 7);
		transform &= ~7;
	}

	return out;
}

uint32_t mortonToHilbert3D(uint32_t mortonIndex, uint32_t bits)
{
	return transformCurve(mortonIndex, bits, mortonToHilbertTable);
}

uint32_t hilbertToMorton3D(uint32_t hilbertIndex, uint32_t bits)
{
	return transformCurve(hilbertIndex, bits, hilbertToMortonTable);
}

The 3D Hilbert curve transforms under the group A4, which has 12 elements. However as there are only 8 transformations that can appear on the left-hand side of each multiplications, only an 8x12 subset of the multiplication table is required. By folding the the index <=> octant mapping function into this table and additionally storing each index respectively octant into the lower 3 bits of each entry, we end up with a compact 96 byte LUT for each function.

These functions can be used as drop-in replacement for the algorithm provided by Fast 2D and 3D Hilbert curves and Morton codes, but are faster by a factor of roughly 2.5 on my machine.